Answer:
The helicopter must cover a straight line distance of approximately 61.270 miles from the hospital to the wreck site.
Explanation:
Let suppose that Air Care helicopter travels in straight line from the hospital to the wreck site, we can determine that distance (
 ), measured in miles, by using the following Pythagorean identity from Analytical Geometry:
), measured in miles, by using the following Pythagorean identity from Analytical Geometry:
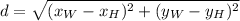
Where:
 ,
,
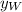 - Location of the wreck site, measured in miles.
- Location of the wreck site, measured in miles.
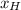 ,
,
 - Location of the hospital, measured in miles.
- Location of the hospital, measured in miles.
If the location of the wreck site and the hospital are
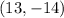 and
and
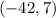 , respectively. The distance that helicopter must cover is:
, respectively. The distance that helicopter must cover is:
![d = \sqrt{[13-(-42)]^(2)+[(-14)-13]^(2)}](https://img.qammunity.org/2021/formulas/mathematics/high-school/ro8tmjtut4gd93rnros68qyh6ryjgkan4b.png)
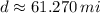
The helicopter must cover a straight line distance of approximately 61.270 miles from the hospital to the wreck site.