Question

What are the transformations? f left parenthesis x right parenthesis space equals negative 3 left parenthesis x minus 4 right parenthesis squared plus 3

Answer 1

Answer:a

Explanation:

Answer 2

The graph of the functions moves 4 units right, 3 units up stretches vertically by a factor of 3 and reflects horizontally.

Explanation:

In order to find the function transformations, we must first determine what the base function is:

`f(x)=x^(2)`

Next, we need to determine how the function is being affected by the transformations.

When the graph of the function moves 4 units right, we mus subtract 4 units from x, so the function looks like this then:

`f(x)=(x-4)^(2)`

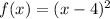
If we need to stretch it vertically by a factor of 3, we need to multiply the function by 3:

`f(x)=3(x-4)^(2)`

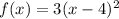
If we need to reflect it horizontally, then we turn the 3 into a negative so we get:

`f(x)=-3(x-4)^(2)`

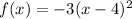
And finally, if we wanted to move the graph up by 3 units, then we need to add 3 units to the whole graph, so we get:

`f(x)=-3(x-4)^(2)+3`

in the attached picture you will be able to see the graph of the base function with all the transformations.