Answer:
(a). The general solution is
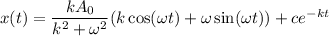
(b). The initial condition does not affect the long term.
Step-by-step explanation:
Given that,
The equation is
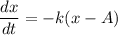
Where, x = temperature
t = time
A = ambient temperature
(a). We need to calculate the general solution
Using given differential equation,
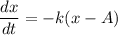 ...(I)
...(I)
Where,
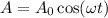
Put the value of A in equation (I)
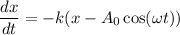
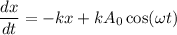
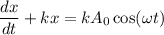 .....(II)
.....(II)
The integrating factor
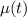 is given by
is given by


Now, multiplying the equation (II) by μ(t) and integrating,
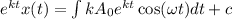
Where, c= constant
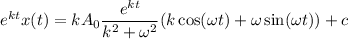
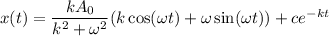 ....(III)
....(III)
(b). We need to find the difference in the long term
Using equation (III)
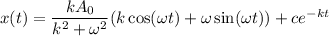
At t = 0,
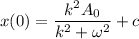
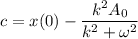
Now, put the value of c in equation (III)
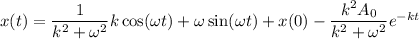
Now,
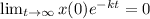
For any x(0) ∈ R
So, the initial condition does not affect the long term.
Hence, (a). The general solution is
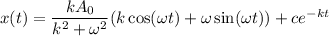
(b). The initial condition does not affect the long term.