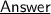
Let's simplify ~

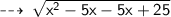
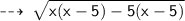
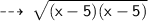
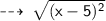
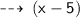
value x lies between :
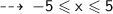
if the value of x is taken -5
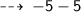

if value of x is taken as 5
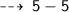
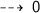
So, the possible values of the required expression lies between ~
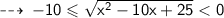
I hope you understood the whole procedure. let me know if you have any doubts in given steps ~