Question

A manufacturer of potato chips would like to know whether its bag filling machine works correctly at the 443 gram setting. It is believed that the machine is underfilling the bags. A 15 bag sample had a mean of 434 grams with a standard deviation of 17. A level of significance of 0.1 will be used. Assume the population distribution is approximately normal. Determine the decision rule for rejecting the null hypothesis. Round your answer to three decimal places.

Answer 1

Null hypothesis

`\mathbf{H_o: \mu = 443}`

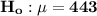
Alternative hypothesis

`\mathbf{H_1 : \mu < 443}`

t = - 2.05

Degree of freedom df = 14

P-value = 0.0298

Decision rule: To reject
`H_o` if significance level ∝ is greater than P-value.

Conclusion: We reject
`H_o` at the level of significance ∝ = 0.1, thus there is sufficient evidence to conclude that the machine is underfilling the bags.

`H_o`

Explanation:

Given that:

Population mean
`\mu` = 443

Sample size n = 15

Sample mean
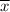`\overline x` = 434

standard deviation
`\sigma` = 17

Level of significance ∝ = 0.01

The null and the alternative hypothesis can be computed as:

Null hypothesis

`\mathbf{H_o: \mu = 443}`

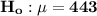
Alternative hypothesis

`\mathbf{H_1 : \mu < 443}`

The t-test statistics can be computed as :

`t = (\overline x - \mu )/((\sigma )/(√(n)))`

`t = (434 -443)/((17)/(√(15)))`

`t = (-9)/((17)/(3.873))`

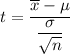
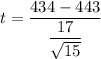
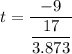
t = - 2.05

Degree of freedom df = n - 1

Degree of freedom df = 15 - 1

Degree of freedom df = 14

From t distribution table; from the area in the lower tail to the left of t = -2.05 and for the degree of freedom df = 14, it is given by 0.0298

Thus, P-value = 0.0298

Decision rule: To reject
`H_o` if significance level ∝ is greater than P-value.

Conclusion: We reject
`H_o` at the level of significance ∝ = 0.1, thus there is sufficient evidence to conclude that the machine is underfilling the bags.

`H_o`