Question

Dr. Thermo, only has one bottle of neon. However, he needs to run two experiments, each requiring its own bottle. Therefore, he plans to connect the two bottles together and open the valves on each so that each bottle is partially filled. He wants to know how the enthalpy of the gas will change when he performs this operation. Each bottle has an internal volume of 43.8 L, is completely rigid, and fully insulated. At the start, the full bottle has a pressure of 1.1 MPa, the second bottle is completely evacuated, and both are at room temperature (298 K). After the valves are opened, the two bottles come to equilibrium at 346 kPa. You can assume that neon behaves ideally during this process.

a. Dr. Thermo wants you to derive an equation for H(P.V) and then use that equation to determine the change in enthalpy by integration, showing him all your work.
b. Being a thermo wiz, you know there is another (and easier) way to perform this calculation. Verify your answer to part a using this easier way.

Answer 1

The data provided in the question are :

`$V_1 = V_2 = 43.8\ L$`

=
`$ (43.8)/(1000)\ m^3$`

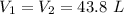
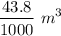
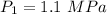`$ P_1 = 1.1\ MPa$` and
`$ P_2 = 0$`

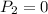
Initial pressure of neon = 1.1 MPa

Final Pressure = 346 kPa

Initial temperature of neon = 298 K

`$P_1V_1=mRT_1$`

`$ 1.1 * 10^6 * (43.8)/(1000) = m * (8314)/(MM)* 298$`

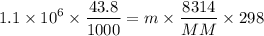
Molecular mass of neon = 20.1797 g/mole

m = 0.3924 kg

For final temperature:

`$P_fV_f=mRT_f$`

`$V_f = 2 * (43.8)/(1000)$`

`$ 346 * 1000 * 2 * (43.8)/(1000) = m * (8314)/(20.1797) * T_f$`

`$ \therefore T_f = 187.48\ K$`

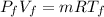
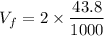
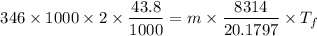
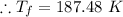
a). From first law of thermodynamics :

δQ = δU + δW

Tds = dU + PdV

or dH = dTs + VdP

As system is insulator, Tds = 0

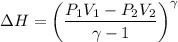`$ \Delta H = \left( (P_1V_1-P_2V_2)/(\gamma - 1) \right)^(\gamma)$` as
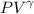`$PV^(\gamma)$` = constant

`$P_1V_1^(\gamma)= PV^(\gamma)$`

`$V= \left( (P_1V_1^(\gamma))/(P) \right)^{(1)/(\gamma)}$`

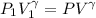
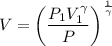
Substituting in VdP and integrating, the above equation is obtained.

So, γ = 1.67 (mono atomic neon)

`$ \Delta H = 1.67 * ((1.1 * 10^6 * 0.0438 - 346 * 10^3 * 2 * 0.0438))/(1.67-1)$`

`$ \Delta H = 44942.63\ J$`

`$ \Delta H = 44.942\ kJ$`

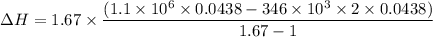
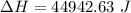
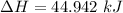
b). Easier way is :

`$ \Delta H = mC_P\Delta T$`

`$ \Delta H = 0.3924 * C_P(T_f-T_1)$`

`$C_P = (\gamma R)/(\gamma-1)$`

`$= (1.67 * 8314)/(0.67 * 20.1797)$`

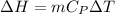
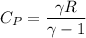
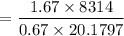
= 1026.92 J/kg-K

`$ \Delta H = 0.3924 * 1026.92 (187.48-298)$`

`$ = -44.585\ kJ$`

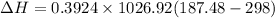
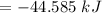
The negative sign indicates decrease in enthalpy.

The answer by easier way is very near to the value in part (a).

Error (%) =
`$ (44.942-44.585)/(44.942) * 100$`

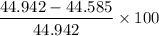
= 0.015 % (which is negligible)

Therefore, both the answers are same.