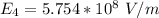Complete Question
Red blood cells can be modeled as spheres of 6.53 μm diameter with −2.55×10−12 C excess charge uniformly distributed over the surface. Find the electric field at the following locations, with radially outward defined as the positive direction and radially inward defined as the negative direction. The permittivity of free space ????0 is 8.85×10−12 C/(V⋅m). What is the electric field
E⃗ 1 inside the cell at a distance of 3.05 μm from the center?
E⃗ 2 Just inside the surface of the cell
E⃗ 3 Just outside the surface of the cell
E⃗ 4 At a point outside the cell 3.05 μm from the surface
Answer:
E⃗ 1
0 V/m
E⃗ 2
0 V/m
E⃗ 3
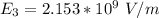
E⃗ 4
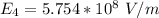
Step-by-step explanation:
From the question we are told that
The diameter is
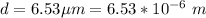
The charge is
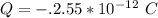
The permittivity of free space is

The distance considered is
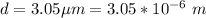
Generally the electric field inside the cell at a distance of 3.05 μm from the center is
0 V/m
This because there is no electric field felt inside the cell according Gauss the cell is taken as a point charge
Generally the electric field just inside the surface of the cell is 0 V/m
This because there is no electric field felt inside the cell according Gauss the cell is taken as a point charge
Generally the electric field just outside the cell is mathematically represented as
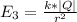
Here
 is the coulomb constant with value
is the coulomb constant with value
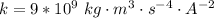
r is the radius of the sphere which is mathematically as
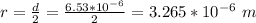
![E_3 = ( 9*10^(9) * |-2.55 *10^(-12) |)/( [3.265 *10^(-6) ]^2 )](https://img.qammunity.org/2021/formulas/physics/college/k8rgxtgs1k88uq9chkdojccljqe5v3410c.png)
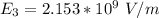
Generally the electric field at a point outside the cell 3.05 μm from the surface is mathematically represented as
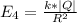
Here R is mathematically represented as
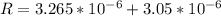
=>
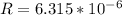
So
![E_4 = ( 9*10^(9) * |-2.55 *10^(-12) |)/( [ 6.315 *10^(-6) ]^2 )](https://img.qammunity.org/2021/formulas/physics/college/wvt3rjumsyskftglfxlzjhzcghkwkvlbyr.png)