Answer:
t = 2212 years
Step-by-step explanation:
In radioactive decay processes it is described by the equation
N = N₀
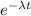
to calculate the activity
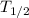 = log 2 /λ
= log 2 /λ
λ = log 2 / T_{1/2}
λ = log 2 /5715
λ = 5.267 10⁻⁵
now the amount of carbon 14 is N₀ = 0.1%, the sample contains an amount of N = 0.089%
N / N₀ = e^{-\lambda t}
-λ t = ln N / N₀
t = - 1 /λ ln N /N₀
t = 1 / 5.267 10⁻⁵ ln (0.089 / 0.1)
t = 2,212 10³ years
t = 2212 years