Question

A local artist working at the town fair makes caricatures and portraits. The caricatures cost $4 to make white

the portraits cost $10 to make. It takes 20 minutes to make a caricature and 30 minutes to make a portrait. The

artist can spend no more than $360 for supplies and can stay no more than 20 hours at the fair. She would like

to charge $10 for a caricature and $20 for a portrait. She is going to donate all proceeds of the weekend fair to a

local charity. How many caricatures and how many portraits should she make in order to maximize the

donation for the charity?


1. Identify the variables for this problem.



2. Write four inequalities that constrain the problem.

Answer 1

The artist should make 15 caricatures and 30 portraits.

Explanation:

First, we identify the variables for the problem. In this case, the variables will be:

C=number of caricatures

P= number of portraits.

Next, we can use the variables to make the inequalities that constrain the problem.

We know the artist can't spend more than $360 for supplies and we also know that it costs $4 to make a caricature and $10 to make a portrait, so:

`4C+10P\le 360`

We also know the artist has a limit of time of 20 hours, which is the same as 20*60=1200 minutes to paint. We know it takes her 20 minutes to make a caricature and 30 minutes to make a portrait, so:

`20C+30P\le 1200`

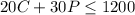
and we also know she must make a positive number of caricatures and a positive number of portraits so the other two constrains are:

`C\ge 0`

`P\ge 0`

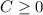
So we can go ahead and graph them. (see attached picture)

Once we graphed the inequalities we can determine what the corners of the polygon created by the intersection of the shaded areas are, so we proceed and calculate them:

first point:

(0,0)

second point:

4(0)+10P=360

`P=(360)/(10)`

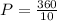
P=36

(0,36)

Third point:

20C+30(0)=1200

`C=(1200)/(20)`

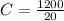
C=60

(60,0)

Fourth point:

`4C+10P = 360`

`20C+30P = 1200`

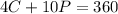
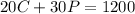
We multiply the first equation by -5 so we get:

-20C-50P=-1800

20C+30P=1200

------------------------

-20P=-600

P=30

so:

20C+30(30)=1200

20C=1200-900

20C=300

C=15

(15,30)

Once we found the 4 points, we go ahead and evaluate them for the objective function. In this case, the objective function is the total amount of money she got from selling the pieces of art, so we get:

I=10C+20P

Point 1

I=10(0)+20(0)=0

Point 2

I=10(0)+20(36)=720

Point 3

I=10(60)+20(0)=600

Point 4

I=10(15)+20(30)=750

Next, we look for the greatest income which in this case will be 750 so that's why she must make 15 caricatures and 30 Portraits.