Answer: (960.80,1039.20)
Explanation:
Let X denotes a random variable that represents the life of the light bulbs produced at the factory.
As per given,
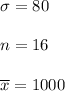
Critical z-value for 95% confidence interval : z* = 1.96
Confidence interval for population mean:

So, a 95% confidence interval estimate (CIE) of the true mean life (m) of light bulbs produced in this factory = (960.80,1039.20)