Question

Assume that each atom is a hard sphere with the surface of each atom in contact with the surface of its nearest neighbor. Determine the percentage of total unit cell volume that is occupied in (a) simple cubic lattice and (b) a diamond lattice. For each case, write down smallest distance, unit volume, number of atoms per unit cell, equation for density or packing fraction. Show your calculation and check your unit.

Answer 1

The classification of the concern is listed in the interpretation segment below.

Step-by-step explanation:

(a)...

Simple cubic lattice

`a=2r`

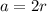
Now,

The unit cell volume will be:

`=a^3`

`=(2r)^3`

`=8r^3`

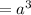
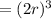
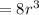
At one atom per cell, atom volume will be:

`=(1)* ((4 \pi r^3)/(3))`

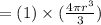
Then the ratio will be:

`Ratio=((4 \pi r^3)/(3))/(8r^3)* 100 \ percent`

`=52.4 \ percent`

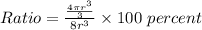
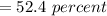
(b)...

Diamond lattice

The body diagonal will be:

`d=8r=a√(3)`

`a=(8)/(√(3))r`

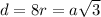
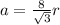
The unit cell volume will be:

`=a^1`

`=((8r)/(√(3)))^1`

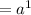
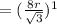
At eight atom per cell, the atom volume will be:

`=8((4 \pi r^1)/(3))`

Then the Ratio will be:

`Ratio=(8((4 \pi r^1)/(3)))/(((8r)/(√(3)))^1)* 100 \ percent`

`=34 \ percent`

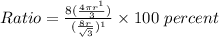
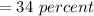
Note: percent = %