Question

A stone is tossed horizontally from the highest point of a 95 m building and lands 105 m from the base of the building. Ignore air resistance, and use a coordinate system whose origin is at the highest point of the building, with positive y upwards and positive x in the direction of the throw.

A. How long is the stone in the air in s?
B. What must have been the initial horizontal component of the velocity, in m/s?
C. What is the vertical component of the velocity just before the stone hits the ground, in m/s?
D. What is the magnitude of the velocity of the stone just before it hits the ground, in m/s?

Answer 1

A) t = 4.40 s , B) v = 23.86 m / s , c) v_y = - 43.12 m / s , D) v = 49.28 m/s

Step-by-step explanation:

This is a projectile throwing exercise,

A) To know the time of the stone in the air, let's find the time it takes to reach the floor

y = y₀ +
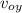`v_(oy)` t - ½ g t²

as the stone is thrown horizontally v_{oy} = 0

y = y₀ - ½ g t²

0 = y₀ - ½ g t²

t = √ (2 y₀ / g)

t = √ (2 95 / 9.8)

t = 4.40 s

B) what is the horizontal velocity of the body

v = x / t

v = 105 / 4.40

v = 23.86 m / s

C) The vertical speed when it touches the ground

v_y =
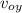`v_(oy)` - g t

v_y = 0 - 9.8 4.40

v_y = - 43.12 m / s

the negative sign indicates that the speed is down

D) total velocity just hitting the ground

v = vₓ i ^ + v_y j ^

v = 23.86 i ^ - 43.12 j ^

Let's use Pythagoras' theorem to find the modulus

v = √ (vₓ² + v_y²)

v = √ (23.86² + 43.12²)

v = 49.28 m / s

we use trigonometry for the angle

tan θ = v_y / vₓ

θ = tan⁻¹ (-43.12 / 23.86)

θ = -61