Question

Vitamin D (delivered naturally by sunshine) helps the human body stay energized and burn fat. Researchers sampled 42 random sunbathers. The average vitamin D level was 27 nanograms per milliliter and the standard deviation was 3 nanograms per milliliter. Construct and interpret a 90% confidence interval to estimate the mean vitamin D level in the population.

Answer 1

Answer: A 90% confidence interval to estimate the mean vitamin D level in the population = (26.22,27.78)

Interpretation: We are 90% confident that the true population mean lies in (26.22,27.78).

Explanation:

Let X denotes a random variable that represents the vitamin D level .

As per given,

`\text{Sample size=}n=42\\\\ \text{Sample mean=}\overline{x}=27\\\\ \text{Sample standard deviation}= s= 3`

Since population standard deviation is unknown , so we will use t -test .

For that, Degree of freedom = df = n-1 = 41

Significance
`\alpha=1-0.90=0.1`

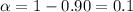
Two-tailed critical t-value :
`t_(\alpha/2,n-1)=t_(0.05,41)=1.683`

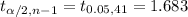
Confidence interval for population mean:

`\overline{x}\pm t_(\alpha/2,n-1)(s)/(√(n))\\\\ =27\pm (1.683)(3)/(√(42))\\\\ =27\pm (1.683)(3)/(6.4807)\\\\=27\pm (1.683)(0.463)\\\\=27\pm0.78\\\\=(27-0.78,\ 27+0.78)\\\\=(26.22,27.78)`

So, a 90% confidence interval to estimate the mean vitamin D level in the population = (26.22,27.78)

Interpretation: We are 90% confident that the true population mean lies in (26.22,27.78).