Answer:
No these these result do not differ at 95% confidence level
Explanation:
From the question we are told that
The first concentrations is

The second concentrations is
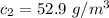
The first sample size is
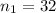
The second sample size is

The first standard deviation is
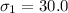
The first standard deviation is
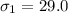
The mean for Turnpike is
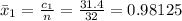
The mean for Tunnel is
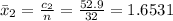
The null hypothesis is
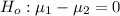
The alternative hypothesis is
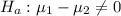
Generally the test statistics is mathematically represented as
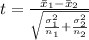
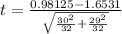
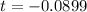
Generally the degree of freedom is mathematically represented as
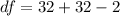
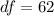
The significance
 is evaluated as
is evaluated as
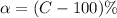
=>
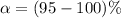
=>

The critical value is evaluated as
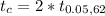
From the student t- distribution table
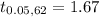
So
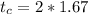
=>

given that
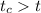 we fail to reject the null hypothesis so this mean that the result do not differ
we fail to reject the null hypothesis so this mean that the result do not differ