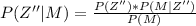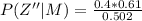Answer:
The value is

Explanation:
From the question we are told that
The proportion that can not find a full time job in their chosen profession is
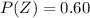
The proportion that can not find a full time job in their chosen profession who are female is
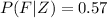
The proportion that can find a full time job in their chosen profession who are female is
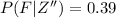
The proportion that cannot find a full time job in their chosen profession who are male is
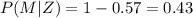
The proportion that can find a full time job in their chosen profession who are male is
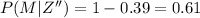
The proportion that can find a full time job in their chosen profession is

Generally the probability that the college graduates is a male is mathematically evaluated using Bayes' Rule as follows
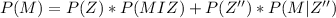
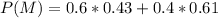
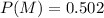
Generally the probability he can find a full time job in his chosen profession is mathematically evaluated using Bayes' Rule as follows