Question

Show whether the pair of lines is parallel, perpendicular, or neither and indicate which. 2x+3y=4 and 2y=3x+17

Answer 1

Explanation:

Hey there!

Here,

The equations are;

2x+3y = 4

2x+3y-4=0..........(i).

2y = 3x + 17

3x -2y +17 =0.......(ii).

Now,

From equation (i).

`slope(m1) = ( - coeff. \: of \: x)/( \: coeff. \: of \: y)`

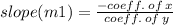
Put values.

`m1 = ( - 2)/(3)`

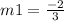
Therefore the slope is-2/3.

From equation (ii).

`slope(m2) = ( - coeff. \: of \: x)/( \: coeff. \: of \: y)`

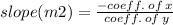
Put value.

`m2 = ( - 3)/( - 2)`

Therefore the slope is 3/2.

For, parallel lines;

m1= m2

-2/3 is not equal to 3/2.

So, they are not parallel lines.

For, perpendicular lines;

m1 × m2 = -1

`( - 2)/(3) * (3)/(2)`

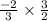
After simplifying it we get, (-1).

Therefore they are perpendicular to eachother.

Hope it helps...