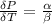Question

The coefficient of thermal expansion α = (1/V)(∂V/∂T)p. Using the equation of state, compute the value of α for an ideal gas. The coefficient of compressibility β is define by β = -(1/V)(∂V/∂p)T. Compute the value of β for an ideal gas. For an ideal gas, express the derivative (∂p/∂T)v in terms of α and β. Do the same derivative for van der Waals gas.

Answer 1

The coefficient of thermal expansion α is

`\alpha  =  (1)/(T)`

The coefficient of compressibility

`\beta   =  (1)/(P)`

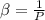
Now considering
`(( \delta P )/(\delta T) )V`

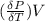
From equation (1) we have that

`( \delta P)/(\delta T) = (n R )/(V)`

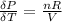
From ideal equation

`nR = (PV)/(T)`

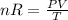
So

`(\delta P)/(\delta T) = (PV)/(TV)`

=>
`(\delta P)/(\delta T) = (P)/(T)`

=>
`(\delta P)/(\delta T) = (\alpha )/(\beta)`

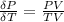
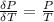
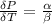
Step-by-step explanation:

From the question we are told that

The coefficient of thermal expansion is
`\alpha = (1)/(V) * ((\delta V)/( \delta P)) P`

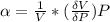
The coefficient of compressibility is
`\beta = - ((1)/(V) ) * ((\delta V)/( \delta P) ) T`

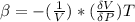
Generally the ideal gas is mathematically represented as

`PV = nRT`

=>
`V = (nRT)/(P) --- (1)`

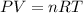
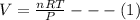
differentiating both side with respect to T at constant P

`(\delta V)/(\delta T ) = ( n R )/(P)`

substituting the equation above into
`\alpha`

`\alpha = (1)/(V) * ( ( n R )/(P)) P`

`\alpha = (nR)/(PV)`

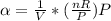
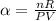
Recall from ideal gas equation
`T = (PV)/(nR)`

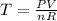
So

`\alpha = (1)/(T)`

Now differentiate equation (1) above with respect to P at constant T

`(\delta V)/( \delta P) = -(nRT)/(P^2)`

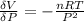
substituting the above equation into equation of
`\beta`

`\beta = - ((1)/(V) ) * (-(nRT)/(P^2) ) T`

`\beta =( ((n RT)/(PV) ))/(P)`

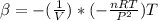
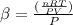
Recall from ideal gas equation that

`(PV)/(nRT) = 1`

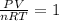
So

`\beta = (1)/(P)`

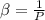
Now considering
`(( \delta P )/(\delta T) )V`

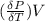
From equation (1) we have that

`( \delta P)/(\delta T) = (n R )/(V)`

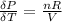
From ideal equation

`nR = (PV)/(T)`

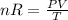
So

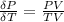
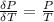
`(\delta P)/(\delta T) = (PV)/(TV)`

=>
`(\delta P)/(\delta T) = (P)/(T)`

=>
`(\delta P)/(\delta T) = (\alpha )/(\beta)`