Question

You are exploring a newly discovered planet. The radius of the planet is 7.20×107m. You suspend a lead weight from the lower end of a light string that is 4.00 m long and has mass 0.0280 kg. You measure that it takes 0.0625 s for a transverse pulse to travel from the lower end to the upper end of the string. On earth, for the same string and lead weight, it takes 0.0390 s for a transverse pulse to travel the length of the string. The weight of the string is small enough that its effect on the tension in the string can be neglected. Assuming that the mass of the planet is distributed with spherical symmetry, what is its mass?

Answer 1

Step-by-step explanation:

velocity of a transverse wave is proportional to root of tension in the string

V α √ T

V = k √ T where k is a constant .

`(V_1)/(V_2) = \sqrt{(T_1)/(T_2) }`

V₁ and V₂ are velocities of wave corresponding to tension of T₁ and T₂ in the string . Let T₁ be tension when the experiment was conducted on new planet and T₂ is tension when it was conducted on the Earth.

Tension will be equal to weight suspended so ,

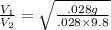`(V_1)/(V_2) = \sqrt{(.028 g )/(.028 * 9.8) }` where g is gravitational acceleration on new planet

V₂ = 4 / .039 = 102.564 m /s

V₁ = 4 / .0625 = 64 m /s

`(64)/(102.564) = \sqrt{(.028 g )/(.028 * 9.8) }`

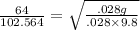
.389 =
`(g)/(9.8)`

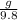
g = 3.8 m /s²

g = G M / R² where G is universal gravitational constant , R is radius

3.8 = 6.67 x 10⁻¹¹ x M / (7.2 x 10⁷ ) ²

M = 29.53 x 10²⁵ kg .