Question

An article claims that 12% of trees are infested by a bark beetle. A random sample of 1,000 trees were tested for traces of the infestation and found that 127 trees were affected.

z = p - p/p q/n
Using the formula and data provided, what is the value of the z-test statistic?

Answer 1

0.70

Explanation:

Answer 2

Answer: 0.6812

Explanation:

Let p be the population proportion of trees are infested by a bark beetle.

As per given: p= 12%= 0.12

Sample size : n= 1000

Number of trees affected in sample = 1000

Sample proportion of trees are infested by a bark beetle. =
`\hat{p}=(127)/(1000)=0.127`

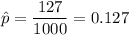
Now, the z-test statistic :
`z=\frac{\hat{p}-p}{\sqrt{(p(1-p))/(n)}}`

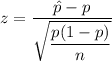
So,
`z=\frac{0.127-0.12}{\sqrt{(0.12* 0.88)/(1000)}}`

`z=\frac{0.007}{\sqrt{(0.1056)/(1000)}}\\\\\\=(0.007)/(√(0.0001056))\\\\\\=(0.007)/(0.010276)\approx0.6812`

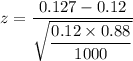
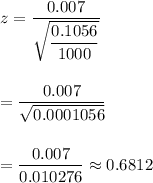
Hence, the value of the z-test statistic = 0.6812 .