Question

Both SAT and ACT are​ well-known placement tests that most US colleges require from prospective students to be admitted in their programs. Scores in the SAT test are approximately normally distributed with a mean of 500 and a standard deviation of 100. Scores in the ACT test are approximately normally distributed with a mean of 18 and a standard deviation of 6. What would be the score in the SAT test to get the same​ z-score as the admission requirement of an ACT score of​ 27?

Answer 1

Answer: 650

Explanation:

Formula for z-score :
`Z=\frac{X-mean}{\text{Standrad deviation}}`

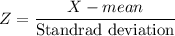
, where X = random variable that follows normal distribution.

Given: ACT test are approximately normally distributed with a mean of 18 and a standard deviation of 6.

For X = 27

`Z=(27-18)/(6)=(9)/(6)=(3)/(2)=1.5`

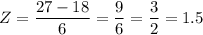
Also, SAT test are approximately normally distributed with a mean of 500 and a standard deviation of 100.

If z-score for both tests are same then,

`1.5=(X-500)/(100)\\\\\Rightarrow\ 1.5*100=X-500\\\\\Rightarrow\ X-500=150\\\\\Rightarrow\ X=150+500\\\\\Rightarrow\ X=650`

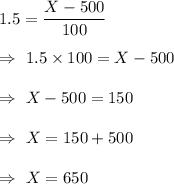
Hence, the required score in SAT test to get the same​ z-score = 650