Question

Review the graph of function g(x). On a coordinate plane, y = g (x) has a straight line connecting point (negative 5, 4) and (negative 2, 1), a curved line connected (negative 2, 1) and (0, negative 1), and a straight line connecting (0, negative 1) and (4, negative 2). Determine the value of g–1(4).

Answer 1

A

Explanation:

Answer 2

Option (1)

Explanation:

From the graph attached,

Points connecting the graph 'g' are (-5, 4), (-2, 1), (0, -1), (4, -2).

Since, rule to get the points lying on the graph of the inverse of the given function is,

(x, y) → (y, x)

If (x, y) is a point on function 'g' then (y, x) will lie on the inverse of the given function.

By the given rule, points on
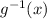`g^(-1)(x)` will be,

(4, -5), (1, -2), (-1, 0), (-2, 4)

Therefore, value of the inverse function at x = 4 will be,

y =
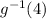`g^(-1)(4)` = -5

Option (1) will be the correct option.