Question

A certain type of concrete mix is designed to withstand 3000 pounds per square inch​ (psi) of pressure. The concrete is poured into casting cylinders and allowed to set for 28 days. The​ concrete's strength is then measured. The following data represent the strength of nine randomly selected casts​ (in psi). Compute the​ mean, median, and mode strength of the concrete​ (in psi).

3960, 4090, 3200, 3100, 2940, 3830, 4090, 4040, 3780

Answer 1

Explanation:

Given the data representation of the strength of nine randomly selected casts​ (in psi) as 3960, 4090, 3200, 3100, 2940, 3830, 4090, 4040, 3780.

MEAN

Mean is the average of the samples

`\overline x = (\sum Xi)/(N)`

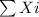`\sum Xi` is thw sum of the given data

N is the sample size

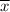`\overline x` is the mean

`\overline x = (3960+4090+3200+3100+2940+3830+4090+4040+3780)/(9)\\\\\overline x = (33,030)/(9)\\ \\\overline x = 3,670psi`

Hence the mean of the data is 3,670psi

MEDIAN

Median is the value at the middle of the data after rearrangement.

On rearranging in ascending order

2940, 3100, 3200, 3,780) 3,830 (3,960, 4040, 4090, 4090

It can be seen that the middle value is 3860. Hence the median of the data is 3860psi.

MODE

Mode is the most occurring data in the dataset. It is the data with the highest frequency. From the data, it can be seen that the only data occurring most (twice) is 4090, hence the modal value is 4090psi