Question

How do you do these two questions?

Answer 1

(a) Solution : 1/8 cot⁻¹(4) or 1/8 tan⁻¹(¼) (either works)

(b) Solution : tan(x)/sin(x) + In | tan(x/2) | + C

Explanation:

(a) We have the integral (x/16 + x⁴)dx on the interval [0 to 1].

For the integrand x/6 + x⁴, simply pose u = x², and du = 2xdx, and substitute:

1/2 ∫ (1/u² + 16)du

'Now pose u as 4v, and substitute though integral substitution. First remember that we have to factor 16 from the denominator, to get 1/2 ∫ 1/(16(u²/16 + 1))' :

∫ 1/4(v² + 1)dv

'Use the common integral ∫ (1/v² + 1)dv = arctan(v), and substitute back v = u/4 to get our solution' :

1/4arctan(u/4) + C

=> Solution : 1/8 cot⁻¹(4) or 1/8 tan⁻¹(¼)

(b) We have the integral ∫ sec³(x)/tan(x)dx, which we are asked to evaluate. Let's start by substitution tan(x) as sin(x)/cos(x), if you remember this property. And sec(x) = 1/cos(x) :

∫ (1/cos(x))³/(sin(x)/cos(x))dx

If we cancel out certain parts we receive the simplified expression:

∫ 1/cos²(x)sin(x)dx

Remember that sec(x) = 1/cos(x):

∫ sec²(x)/sin(x)dx

Now let's start out integration. It would be as follows:

`\mathrm{Let:u=(1)/(\sin \left(x\right)),\:v'=\sec ^2\left(x\right)}\\=> (\tan \left(x\right))/(\sin \left(x\right))-\int \:-\cot \left(x\right)\csc \left(x\right)\tan \left(x\right)dx\\\\\int \:-\cot \left(x\right)\csc \left(x\right)\tan \left(x\right)dx=-\ln \left|\tan \left((x)/(2)\right)\right|\\=> (\tan \left(x\right))/(\sin \left(x\right))-\left(-\ln \left|\tan \left((x)/(2)\right)\right|\right)\\`

`=> (\tan \left(x\right))/(\sin \left(x\right))+\ln \left|\tan \left((x)/(2)\right)\right|\\\\=> (\tan \left(x\right))/(\sin \left(x\right))+\ln \left|\tan \left((x)/(2)\right)\right|+C`

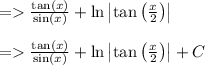
Solution: tan(x)/sin(x) + In | tan(x/2) | + C

Answer 2

(a) ⅛ tan⁻¹(¼)

(b) sec x − ln│csc x + cot x│+ C

Explanation:

(a) ∫₀¹ x / (16 + x⁴) dx

∫₀¹ (x/16) / (1 + (x⁴/16)) dx

⅛ ∫₀¹ (x/2) / (1 + (x²/4)²) dx

If tan u = x²/4, then sec²u du = x/2 dx

⅛ ∫ sec²u / (1 + tan²u) du

⅛ ∫ du

⅛ u + C

⅛ tan⁻¹(x²/4) + C

Evaluate from x=0 to x=1.

⅛ tan⁻¹(1²/4) − ⅛ tan⁻¹(0²/4)

⅛ tan⁻¹(¼)

(b) ∫ (sec³x / tan x) dx

Multiply by cos x / cos x.

∫ (sec²x / sin x) dx

Pythagorean identity.

∫ ((tan²x + 1) / sin x) dx

Divide.

∫ (tan x sec x + csc x) dx

Split the integral

∫ tan x sec x dx + ∫ csc x dx

Multiply second integral by (csc x + cot x) / (csc x + cot x).

∫ tan x sec x dx + ∫ csc x (csc x + cot x) / (csc x + cot x) dx

Integrate.

sec x − ln│csc x + cot x│+ C