Question

Suppose 3.005 g of a nonvolatile solute is added to 20.02 g of water (the solvent), and the boiling point increases from 100.000 OC to 101.286 OC. Determine the TB, molality, moles, and molecular weight for the solute if kb for water is 0.512 OC/m. Report each value using the correct number of significant digits. Refer to Example 1.2 and pages 3-4 in the chapter 1 notes for general chemistry 1 to understand significant figures.

Answer 1

*
`\Delta T_B=1.286\°C`

*
`m=2.5m`

*
`n=0.05mol`

*
`M=59.76g/mol`

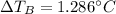
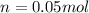
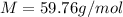
Step-by-step explanation:

Hello,

In this case, considering the boiling point rise problem, we consider its appropriate equation:

`\Delta T_B=imK_b`

Whereas i is the van't Hoff factor that for this nonvolatile solute is 1, m is the molality, Kb the boiling point constant of water as it is the solvent and ΔT the temperature difference. In such a way, with the given information we obtain:

- ΔT:

`\Delta T_B=101.286\°C-100.000\°C\\\\\Delta T_B=1.286\°C`

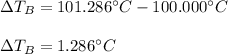
- Molality (mol/kg):

`m=(\Delta T_B)/(i*K_b)=(1.286\°C)/(1*0.512\°C/m)\\ \\m=2.5m`

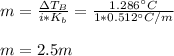
- Moles for 20.02 g (0.02002 kg) of water:

`n=2.5mol/kg*0.02002kg\\\\n=0.05mol`

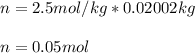
- Molar mass:

`M=(mass)/(moles)=(3.005g)/(0.050mol) \\\\M=59.76g/mol`

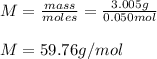
Best regards.