Question

Can someone explain this step by step for me? its from a review so ignore my wrong answer. Thank you!

Answer 1

`P(\text{Male}|\text{Divorced})\approx0.092`

Explanation:

`\displaystyle P(\text{Male}|\text{Divorced})=\frac{P(\text{Male and Divorced})}{P(\text{Male})}=((9.6)/(214.7))/((104.5)/(214.7))\approx0.092`

We can even break this down further by simply only looking at the total amount of males, and finding the proportion of males that are divorced, which is
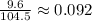`(9.6)/(104.5)\approx0.092`, the same value.

Note that P(Male | Divorced) means the probability of choosing a male, given (|) that person is divorced.