Answer:
a) La función del volumen del depósito está dada por
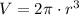 , b) Las dimensiones del depósito de 100 litros de capacidad son: Radio = 25.15 centímetros, Altura = 50.30 centímetros.
, b) Las dimensiones del depósito de 100 litros de capacidad son: Radio = 25.15 centímetros, Altura = 50.30 centímetros.
Explanation:
a) Sabemos por Geometría que el volumen de un cilindro recto (
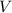 ), medido en decímetros cúbicos o litros, es: (Nótese que 1 litro equivale a un decímetro cúbico)
), medido en decímetros cúbicos o litros, es: (Nótese que 1 litro equivale a un decímetro cúbico)
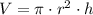
Donde:
 - Radio del área transversal del cilindro, medido en decímetros.
- Radio del área transversal del cilindro, medido en decímetros.
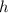 - Altura del cilindro, medida en decímetros.
- Altura del cilindro, medida en decímetros.
Si
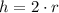 , entonces la fórmula de volumen es:
, entonces la fórmula de volumen es:
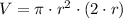
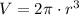
La función del volumen del depósito está dada por
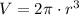 .
.
b) Si sabemos que
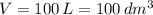 , entonces el radio se obtiene al ser despejado de la función hallada en a).
, entonces el radio se obtiene al ser despejado de la función hallada en a).
![r = \sqrt[3]{(V)/(2\pi) }](https://img.qammunity.org/2021/formulas/mathematics/high-school/nh39j96nl19r1r5jhwkwy7vrvz5kqiqdcn.png)
![r = \sqrt[3]{(100\,dm^(3))/(2\pi) }](https://img.qammunity.org/2021/formulas/mathematics/high-school/a0jysi4dz8utc0m316kc66cdf4t5xfce1r.png)
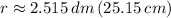
Ahora, la altura, medida en decímetros, se obtiene a continuación:
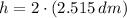
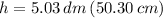
Las dimensiones del depósito de 100 litros de capacidad son: Radio = 25.15 centímetros, Altura = 50.30 centímetros.