Question

For an atmospheric pressure of 97.3 kPa (abs) determine the heights of the fluid columns in barometers containing one of the following liquids: (a) mercury, (b) water, and (c) ethyl alcohol. Calculate the heights, including the effect of vapor pressure, and compare the results with those obtained neglecting vapor pressure ((d), (e), (f)). (g) Do these results support the widespread use of mercury for barometers

Answer 1

Follows are the solution to this question:

Step-by-step explanation:

In the given question firstly we need to calculate the height of the pressure formula with in the vapor pressure, that includes the pressure, and its formula is:

`p(atm)_(vp) = \gamma .h +P_(vp)`

`\to \boxed{ h = (p(atm)_(vp) - p_(vp))/(\gamma)}`

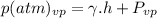
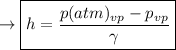
The vapour pressure where
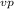`_(vp)` pays any attention. Next mercury measurement,Ethyl alcohol and water.

for mercury calculation:

a)

`h_(Hg \ vp ) =(101 * 10^3 (N)/(m^2)- 1.6 * 10^(-1) (N)/(m^2))/(133 * 10^3 (N)/(m^3))`

`=(101000- 0.16 )/(133000)\\\\ =(100999.84)/(133000)\\\\= 0.759`

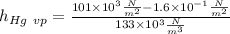
In the next step we calculate water value:

b)

`h_{H_(2)0 \ vp } =(101 * 10^3 (N)/(m^2)- 1.77 * 10^(3) (N)/(m^2))/(9.80 * 10^3 (N)/(m^3))`

`=(101000- 1770)/(9800)\\\\=(99230)/(9800)\\\\= 10.125`

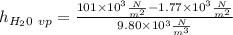
In the last step, now we calculate the value of ethyl alchohol:

c)

`h_(EA \ vp ) =(101 * 10^3 (N)/(m^2)- 5.9 * 10^(3) (N)/(m^2))/(7.74 * 10^3 (N)/(m^3))`

`=(101000 - 5900 )/(7740)\\\\ =(95100 )/(7740)\\\\=12.286`

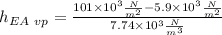
The following would be the precise measurement of the heights without

Pressure of the vapour:

`a) h_(Hg) = (101* 10^3 (N)/(m^2))/(133* 10^3 (N)/(m^3)) \\\\`

`= (101 000 )/(133000 ) \\\\= (101)/(133 ) \\\\= 0.759`

`\\\\b) h_{H_(2) o} = (101* 10^3 (N)/(m^2))/(9.80 * 10^3 (N)/(m^3))`

`= (101)/(9.80 )\\\\=10.30`

`\\\\c) h_(EA) = (101* 10^3 (N)/(m^2))/(7.74 * 10^3 (N)/(m^3))`

`= (101)/(7.74 ) \\\\=13.04`

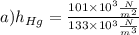
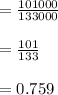
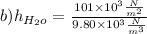
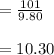
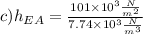
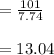
It may draw the substantial inference from of the calculated values. For the very first time. Mercury indicators and vapour pressure effects are insignificant and necessary height is within acceptable values for the mercury barometer tube (imagine). The alcohol barometer tube 12 metres high!).