Question

The digit 5 appears twice in the number 255,120. How does the total value of the 5 on the right compare to the total value of the 5 on the left?

Answer 1

What this person above said

Answer 2

The value of the first "
`5`" in the number
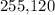`255,\!120` is ten times that of the second "
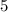`5\!`" in this number.

Explanation:

What gives the number "
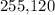`255,\!120`" its value? Of course, each of its six digits has contributed. However, their significance are not exactly the same. For example, changing the first
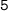`\verb!5!` to
`\verb!6!` would give
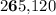`2\mathbf{6}5,\!120` and increase the value of this number by
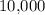`10,\!000`. On the other hand, changing the second
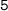`\verb!5!\!` to
`\verb!6!\!` would give
`25\mathbf{6},\!120`, which is an increase of only
`1,\!000` compared to the original number.

The order of these two digits matter because the number "
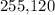`255,\!120`" is written using positional notation. In this notation, the position of each digits gives the digit a unique weight. For example, in
`255,\!120\!`:

`\begin{array}c\cline{1-7}\verb!Digit!& \verb!2! & \verb!5! & \verb!5! & \verb!1! & \verb!2! & \verb!0!\\\cline{1-7}\textsf{Index} & 5 & 4 & 3 & 2 & 1& 0 \\ \cline{1-7} \textsf{Weight} & 10^(5) & 10^(4) & 10^(3) & 10^(2) & 10^(1) & 10^(0)\\\cline{1-7}\end{array}`.

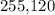(Note that the index starts at
`0` from the right-hand side.)

Using these weights, the value
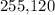`255,\!120` can be written as the sum:

`\begin{aligned}& 255,\!120\\ &= 2 * 10^(5) + 5 * 10^(4) + 5 * 10^(3) + 1 * 10^(2) + 2 * 10^(1) + 0 * 10^(0) \\&=200,\!000 + 50,\!000 + 5,\!000 + 100 + 20 + 0 \end{aligned}`.

As seen in this sum, the first "
`5`" contributed
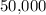`50,\!000` to the total value, while the second "
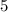`5\!`" contributed only
`5,\!000`.

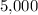Hence: The value of the first "
`5`" in the number
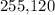`255,\!120` is ten times that of the second "
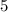`5\!`" in this number.