Question

HELPPPPPPP PLEASEEE

Passing through (-1, -2) and perpendicular to the line whose equation is y + 6 =4/5 (x-5) write an equation in slope intercept form

Answer 1

Explanation:

Hey there!

Given,

The line is passing through point (-1,-2) and perpendicular to the line (y+6) = 4/5(x-5).

Now,

The equation of a st.line passing through point (-1,-2) is,

`(y - y1) = m1(x - x1)`

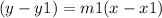
Put all values.

`(y + 2) = m1(x + 1)`

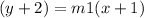
It is the 1st equation.

Another equation is (y+6)= 4/5(x-5).

`y = (4)/(5) x - 10`

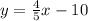
From equation (ii) {After comparing the equation with y =mx+c}.

We get,

M2= 4/5.

Now,

As per the condition of perpendicular lines,

m1×m2= -1.

`m1 * (4)/(5) = - 1`

Simplify them to get answer.

`4m1 = - 5`

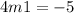
Therefore the slope is, -5/4.

Now, keep the slope in 1st equation.

`(y + 2) = ( - 5)/(4) (x + 1)`

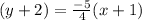
Simplify them to get answer.

`(y + 2) = ( - 5)/(4) x - (5)/(4)`

`y = ( - 5)/(4) x - (5)/(4) - 2`

`y = ( - 5)/(4) x - (13)/(4)`

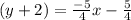
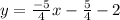
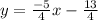
Therefore the required equation is y = -5/4x -13/2.

Hopeit helps....

Answer 2

y = -
`(5)/(4)` x -
`(13)/(4)`

Explanation:

The equation of a line in point- slope form is

y - b = m(x - a)

where m is the slope and (a, b) a point on the line

y + 6 =
`(4)/(5)`(x - 5) ← is in point- slope form

with slope m =
`(4)/(5)`

Given a line with slope m then the slope of a line perpendicular to it is

`m_(perpendicular)` = -
`(1)/(m)` = -
`(1)/((4)/(5) )` = -
`(5)/(4)`

The equation of a line in slope- intercept form is

y = mx + c ( m is the slope and c the y- intercept )

Here m = -
`(5)/(4)` , thus

y = -
`(5)/(4)` x + c ← is the partial equation

To find c substitute (- 1, - 2) into the partial equation

- 2 =
`(5)/(4)` + c ⇒ c = - 2 -
`(5)/(4)` = -
`(13)/(4)`

y = -
`(5)/(4)` x -
`(13)/(4)` ← equation of perpendicular line