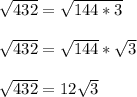Answer:
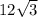
On a keyboard, you would write 12*sqrt(3)
==============================================
Step-by-step explanation:
Find the prime factorization of 432 to get
432 = 2^4*3^3
That allows us to do the following steps
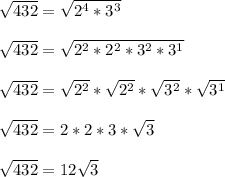
------------------
Or you could do something like this