Question

Please solve this puzzle

Answer 1

Find b

• √16+9
• √25
• 5

#a

Area

• b²
• 5²
• 25m²

H

#b

Done already

• I

#c

• √144-81
• √63
• c=7.94

A

#d

• 1/2(7.94)(9)
• 35.73m²

B

Code is

• HIAB

Answer 2

a = 25 m²

b = 5 m

c = 7.94 m

d = 35.73 m²

Code: H I A B

Explanation:

Formulae

Pythagoras’ Theorem:
`a^2+b^2=c^2`

(where a and b are the legs, and c is the hypotenuse, of a right triangle)

Area of a square = x² (where x is the side length)

------------------------------------------------------------------------------------------------------

Assuming that all the quadrilaterals are squares.

Side length of blue square with area 16 m² = √16 = 4 m

Side length of yellow square with area 9 m² = √9 = 3 m

Use Pythagoras' Theorem to find the length of b:

`\implies 4^2+3^2=b^2`

`\implies b^2=25`

`\implies b=√(25)`

`\implies b=5\: \sf m`

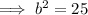
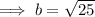
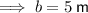
Now we have found length b, we can find area a:

`\textsf{Area a}=b^2=5^2=25\: \sf m^2`

Side length of purple square with area 144 m² = √144 = 12 m

Side length of green square with area 81 m² = √81 = 9 m

Use Pythagoras' Theorem to find the length of c:

`\implies 9^2+c^2=12^2`

`\implies c^2=63`

`\implies c=√(63)`

`\implies c=3√(7)`

`\implies c=7.94\: \textsf{(nearest hundredth)}`

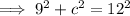
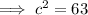
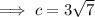
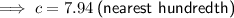
Now we have found length d, we can find area d:

`\textsf{Area d}=(1)/(2)(9)(7.94)=35.73\: \sf m^2`

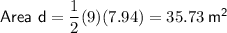
Code: H I A B