Question

What is the volume of a hemisphere with a diameter of 8 ft, rounded to the nearest

tenth of a cubic foot?

Answer 1

We have to find the volume of the hemisphere whose diameter is given, and we have to round off to nearest tenth of a cubic foot.

GiveN:

• Diameter of Hemisphere = 8 ft

The formula for finding the volume of hemisphere is given by:

`v = (2)/(3) \pi {r}^(3)`

Here, r is the radius of Hemisphere.

We have,

⇛ Diameter of hemisphere = 8 ft

⇛ Radius of hemisphere = Diameter / 2

⇛ Radius of the Hemisphere = 8 ft /2 = 4 ft

Finding volume,

`v = (2)/(3) * (22)/(7) * {4}^(3) \: {ft}^(3)`

`v = (2)/(3) * (22)/(7) * 64 \: {ft}^(3)`

`v = (2816)/(21) {ft}^(3)`

`v \approx \: 134.09 \: {ft}^(3)`

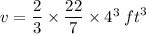
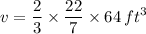
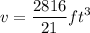
Rounding off to nearest tenth:

`\large{ \boxed{ \bf{ \red{134.1 \: {ft}^(3) }}}}`

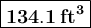
And we are done !!

#CarryOnLearning...

━━━━━━━━━━━━━━━━━━━━

Answer 2

The answer is

134 ft³

Explanation:

Volume of a hemisphere is given by

`V = (2)/(3) \pi {r}^(3)`

where

r is the radius of the hemisphere

From the question

diameter = 8 ft

radius = 8/2 = 4 ft

Substitute the value into the above formula and solve

`V = (2)/(3) ( {4})^(3) \pi \\ = (2)/(3) * 64\pi8 \\ = (128\pi)/(3) \: \: \: \: \: \: \: \\ = 134.0412`

We have the final answer as

134.0 ft³ to the nearest tenth

Hope this helps you