Question

A 32 percent of U.S adults indicated that they have been for HIV at some point in their life. Consider a simple random sample of 15 adults selected at the same time. Find the probability that the number of adults who have been tested for HIV in the sample would be:________

a. Three
b. Between five and nine, inclusive
c. More than five, but less than 10
d. Six or more
e. Less than five
f. Find the mean and the variance of the number of people tested for HIV in samples of size 15.

Answer 1

Answer: a) P(3) = 0

b) P(5<x<9) = 1.28

c) P(5<x<10) = 1.6

d) P(6) or P(x>6) = 2.88

e) P(x<5) = 1.28

f) E(x) = 8

V(x) = 16.34

Explanation: Uniform Distribution is a continuous probability distribution in which probability is constant. It is also known as Rectangular Distribution because of the format the graph makes with the axis.

In this case, the probability of adults had been tested for HIV is 0.32.

Let x be the number of adults tested for HIV:

a) x=3

P(x=3) = 0

The graph is a line paralel to x-axis. To calculate probability, you have to calculate the area under the line. Since there is only one point on the x-axis, there is no variation, so probability is 0.

b) 5<x<9

P(5<x<9) = (9-5)*0.32

P(5<x<9) = 1.28

c) 5<x<10

P(5<x<10) = (10-5)*0.32

P(5<x<10) = 1.6

d) x=6 or x>6

P(x=6) = 0

P(6<x<15) = (15-6)*0.32

P(6<x<15) = 2.88

Using "or" rule:

P(6) + P(6<x<15) = 0 + 2.88 = 2.88

e) x<5

P(1<x<5) = (5-1)*0.32

P(1<x<5) = 1.28

f) Mean or expected value for uniform distribution is

`E(x) = (b+a)/(2)`

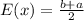
where a and b are the "limits" of the distribution

In the above case, number of adults tested is between 1 and 15. Then

`E(x) = (15+1)/(2)`

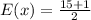
E(x) = 8

Variance of uniform distribution is

`V(x)=(1)/(12) (b-a)^(2)`

`V(x)=(1)/(12) (15-1)^(2)`

`V(x)=(14^(2))/(12)`

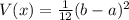
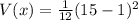
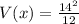
V(x) = 16.34