Answer:
482/999
Explanation:
Since there are 3 repeating digits, starting at the decimal point, the short answer is that the fraction is ...
482/999
where 999 has a number of 9's equal to the number of repeating digits.
This fraction cannot be reduced.
_____
Long answer
Multiply the value by 1000 = 10^3, where the '3' is the number of repeating digits. Then subtract the original and divide by the coefficient of 'x'.
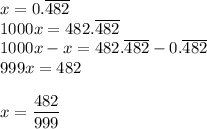
482 and 999 have no common factors, so the fraction cannot be reduced.