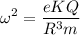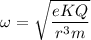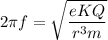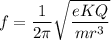Solution :
We assume that there is a ring having a charge +Q and radius r. Electric field due to the ring at a point P on the axis is given by :

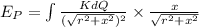
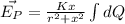

If we put an electron on point P, then force on point e is :
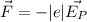
![F= (-eKQx)/((r^2+x^2)^(3/2))= (-eKQx)/(r^3[1+(x^2)/(r^2)]^(3/2))](https://img.qammunity.org/2021/formulas/physics/college/35fieyp459hkn9k7iv1ur0vyir38xe4tjt.png)
If r >> x , then
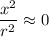
Then,
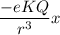
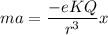

Compare, a = -ω²x
We get,