Question

To complete a project you can either buy a machine at the beginning of a 4 year period, or hire 10 employees at the beginning of a 4 year period. Employee costs (salary and benefits) are $5, 000 at the end of each month for 4 years. You can sell the machine at the end of 4 years for 20% of its original purchase price. What is the maximum price that it makes sense to pay for the machine if effective monthly interest is at j

Answer 1

The company could pay at most $ 187,083.73 for the machine

Missing information:

effective monthly interest rate j = 0.4%

Step-by-step explanation:

We calculate the present value of the employee's salaries using the annuity formula

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 5,000.00

time 48 (4 years x 12 month per year

rate 0.004 (0.4% = 0.4 / 100 = 0.004)

`5000 * (1-(1+0.004)^(-48) )/(0.004) = PV\\`

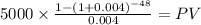
PV $217,971.2447

Now the PV factor of 0.20 of a dollar to represent the 20% of the machine cost being recovered after four years:

`(Maturity)/((1 + rate)^(time) ) = PV`

Maturity $0.20

time 48.00

rate 0.00400

`(0.2)/((1 + 0.004)^(48) ) = PV`

PV 0.1651

now, we construct the equation:

217,971,25 - 0.1651X = X

When X is the maximum amount we could purchase the machine.

217,971,25 = X ( 1 + 0.1651)

217,971,25 / 1.1651 = X

X = $ 187.083,7267

We verify this:

Cost less PV of the salaries plus PV of the residual value = 0

`(Maturity)/((1 + rate)^(time) ) = PV`

Maturity $ 187,083.73 x 20% = $37,416.74

time 48.00

rate 0.00400

`(37416.741)/((1 + 0.004)^(48) ) = PV`

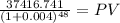
PV of the residual value 30,892.1221

Net present value of the investment:

187.083,70- 217,971.25 + 30,892.1221 ≅ 0

as there is rounding involve there is a minimal difference but we can be satisfy with the answer.