Complete Question
The complete question is shown on the first uploaded image
Answer:
The null hypothesis is rejected this means that
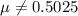
The 95% confidence interval is

Explanation:
From the question we are told that
The standard deviation is s= 0.0001
The sample size is n = 25
The sample mean is
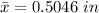
The population mean is
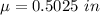
The null hypothesis is

The alternative hypothesis is
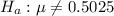
The test statistics is mathematically represented as
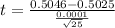
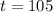
So the p-value from the z-table is mathematically represented as
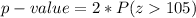
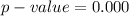
seeing that
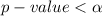 we reject the null hypothesis
we reject the null hypothesis
The critical value of
 obtained from the normal distribution table is
obtained from the normal distribution table is
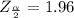
The margin of error is mathematically represented as
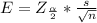
=>
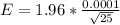
=>
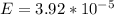
The 95% confidence level is mathematically represented as
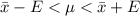
=>
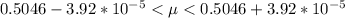
=>
