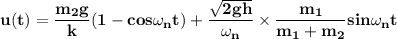Question

A mass m1 hangs from a spring k and is in static equilibrium. A second mass m2 drops through a height h and sticks to m1 without rebound. Determine the subsequent motion u(t) measured from the static equilibrium position of m1 and k.

Answer 1

`\mathbf{u(t) =(m_2g )/(k)(1 - cos \omega_n t) + (√(2gh))/(\omega_n)* (m_1)/(m_1+m_2)sin \omega _n t}`

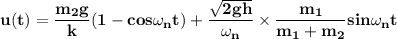
Step-by-step explanation:

From the information given:

The equation of the motion can be represented as:

`(m_1 +m_2) \hat u + ku = m_2 g--- (1)`

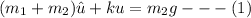
where:

`m_1` = mass of the body 1

`m_2` = mass of the body 2

`\hat u` = acceleration

k = spring constant

u = displacement

g = acceleration due to gravity

Recall that the formula for natural frequency
`\omega _n = \sqrt{(k)/(m_1+m_2)}`

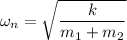
And the equation for the general solution can be represented as:

`u(t) = A cos \omega_nt + B sin \omega _n + (m_2g)/(k) --- (2)`

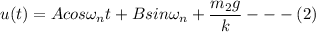
To determine the initial velocity, we have:

`\hat u_2^2 = 2gh`

`\hat u_2 = √(2gh)`

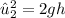
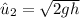
where h = height

Suppose we differentiate equation (2) with respect to time t; we have the following illustration:

`\hat u (t) = - \omega_n A sin \omega_n t+ \omega_n B cos \omega _n t + 0`

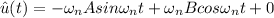
now if t = 0

Then

`\hat u (0) = - \omega_n A sin \omega_n (0)+ \omega_n B cos \omega _n (0) + 0`

`= \omega _n B`

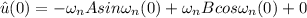
Using the law of conservation of momentum on the impact;

`m_2 \hat u_2=(m_1+m_2) \hat u (0)`

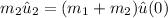
By replacing the value of
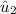`\hat u_2` with
`\sqrt{2gh`

Then the above equation becomes:

`m_2 * √(2gh)=(m_1+m_2) \ u(0)`

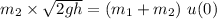
Making u(0) the subject of the formula, we have:

`u(0)= ( m_2 * √(2gh))/((m_1+m_2))`

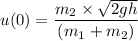
Similarly, the value of the variable can be determined as follows;

Using boundary conditions

`0 = A cos 0 + B sin 0 + (m_2g)/(k)`

`0 = A (1)+0+ (m_2g)/(k)`

`A =- (m_2g)/(k)`

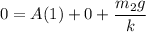
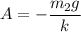
Also, if
`\hat u (0) = \omega_nB`

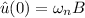
Then :

`(m_2)/(m_1+m_2)√(2gh) = \omega_n B`

making B the subject; we have:

`B = (m_2)/(m_1 + m_2)(√(2gh))/(\omega_n)`

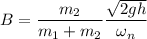
Finally, replacing the value of A and B back to the general solution at equation (2); we have the equation of the subsequent motion u(t) which is:

`\mathbf{u(t) =(m_2g )/(k)(1 - cos \omega_n t) + (√(2gh))/(\omega_n)* (m_1)/(m_1+m_2)sin \omega _n t}`