Question

George is making a triangular enclosure in his yard. He plans on using two old fence posts as vertices, and will place a new

fence post for the third vertex. The old posts are located at (-5, 4) and (2,6), where the coordinates are given in feet. If he
has 25 feet of wire fencing available to close off the area, which of the following are possible locations for the third fence post?
Select the two correct answers. (1 point)
(2,-6)
0 (-9,1)
0 (0,0)
O (8,8)
0 (-4,-5)

Answer 1

The correct answers for the possible locations for the are;

(-9, 1)

(0, 0)

Explanation:

The coordinates of two of the three posts are given in feet as (-5, 4) and (2, 6)

The length of the available fencing = 25 feet

The length, l, of the segment between the coordinates of the two old posts vertices of the fence is given by the following equation;

`l = \sqrt{\left (y_(2)-y_(1) \right )^(2)+\left (x_(2)-x_(1) \right )^(2)}`

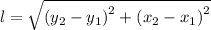
Where;

(x₁, y₁) = (-5, 4)

(x₂, y₂) = (2, 6)

`l = \sqrt{\left (6-4 \right )^(2)+\left (2-(-5) \right )^(2)} = √(53) \approx 7.25 \ feet`

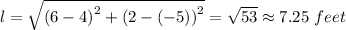
Given the coordinates of the third point as (x₃, y₃), we have;

Therefore, we have;

`\sqrt{\left (y_(3)-4 \right )^(2)+\left (x_(3)-(-5) \right )^(2)} + \sqrt{\left (y_(3)-6 \right )^(2)+\left (x_(3)-(2) \right )^(2)} = 25 - √(53)`

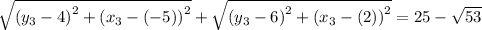
For the point (2, 6), we have;

`\sqrt{\left ((-6)-4 \right )^(2)+\left (2-(-5) \right )^(2)} + \sqrt{\left ((-6)-6 \right )^(2)+\left (2-(2) \right )^(2)} = 24.2 > 25-√(53)`

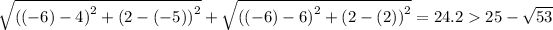
For the point (-9, 1), we have;

`\sqrt{\left ((-6)-4 \right )^(2)+\left (2-(-5) \right )^(2)} + \sqrt{\left ((-6)-6 \right )^(2)+\left (2-(2) \right )^(2)} = 17.08 < 25-√(53)`

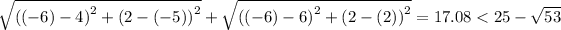
For the point (0, 0), we have;

`\sqrt{\left ((0)-4 \right )^(2)+\left (0-(-5) \right )^(2)} + \sqrt{\left ((0)-6 \right )^(2)+\left (0-(2) \right )^(2)} = 12.73 < 25-√(53)`

For the point (8, 8), we have;

`\sqrt{\left ((8)-4 \right )^(2)+\left (8-(-5) \right )^(2)} + \sqrt{\left ((8)-6 \right )^(2)+\left (8-(2) \right )^(2)} = 19.92 > 25-√(53)`

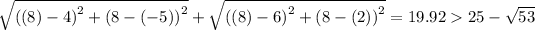
For the point (-4, -5), we have;

`\sqrt{\left ((-5)-4 \right )^(2)+\left ((-4)-(-5) \right )^(2)} + \sqrt{\left ((-5)-6 \right )^(2)+\left ((-4)-(2) \right )^(2)} = 22.04 > 25-√(53)`

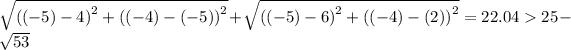
Therefore, the correct answers for the possible locations for the are (-9, 1) and (0, 0).