Given:
Equation of line
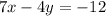 .
.
To find:
The equation of line that goes through the point ( − 21 , 2 ) and is perpendicular to the given line.
Solution:
The given equation of line can be written as
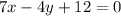
Slope of line is
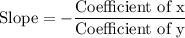

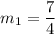
Product of slopes of two perpendicular lines is -1. So, slope of perpendicular line is
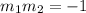
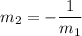
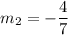
![[\because m_1=(7)/(4)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/2f8vobbrhi00odvlr4qbstguhdvur2z65o.png)
Now, the slope of perpendicular line is
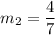 and it goes through (-21,2). So, the equation of line is
and it goes through (-21,2). So, the equation of line is
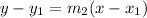
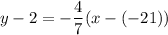
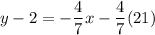
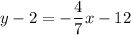
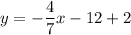
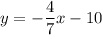
Therefore, the required equation in slope intercept form is
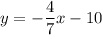 .
.