Given:
The point (9,-12) is on terminal side of angle theta in standard position.
To find:
The exact value of each of the six trigonometric functions of theta.
Solution:
The given point is (9,-12). Here, x-coordinate is positive and y-coordinate is negative. So, the point lies in 4th quadrant and only cos and sec are positive in 4th quadrant.
We know that,
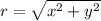
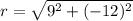
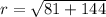
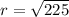
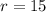
Now,
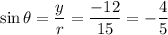
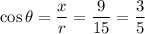
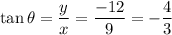
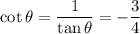
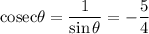
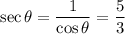
Therefore, the values of six trigonometric functions of theta are
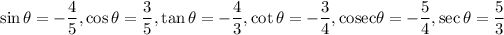 .
.