Question

An observer O is standing on a platform of length L = 90 m on a station. A rocket train passes at a relative (constant) speed of 0.96c moving parallel to the edge of the platform. Then, the observer O found that the front and back of the rocket train simultaneously line up with the ends of the plat form at a particular instant.

A. In the rest frame of the observer O, what is the time necessary for the rocket train to pass a particular point on the platform?
B. What is the rest length lo of the rocket train?
C. According to another observer O on the rocket train, what is the length L of the platform?
D. Again, according to observer O' on the rocket train, how long does it take for observer O to pass the entire length of the rocket train?

Answer 1

Step-by-step explanation:

Since the front and back of the rocket simultaneously line up with forward and backward end of the platform respectively .

Then length of the platform = length of the train rocket .

A )

Time to cross a particular point on the platform

= length of rocket train / .96 x 3 x 10⁸

= 90 / .96 x 3 x 10⁸

= 31.25 x 10⁻⁸ s

B) Rest length of the rocket = length of platform = 90 m

C ) length of platform as viewed by moving observer =

`\frac{90}{\sqrt{1-(v^2)/(c^2 ) } }`

=
`\frac{90}{\sqrt{1-(0.92)/(1 ) } }`

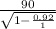
= 321 m

D ) For the observer on platform time taken = 31.25 x 10⁻⁸ s

for the observer in the rocket , time will be dilated so time recorded by observer in motion ,

`31.25*10^(-8) * \sqrt{1-(.96^2)/(1) }`

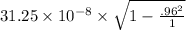
8.75 x 10⁻⁸ s .