Question

A manufacturer of banana chips would like to know whether its bag filling machine works correctly at the 419 gram setting. It is believed that the machine is underfilling the bags. A 19 bag sample had a mean of 412 grams with a variance of 784. A level of significance of 0.025 will be used. Assume the population distribution is approximately normal. Is there sufficient evidence to support the claim that the bags are underfilled

Answer 1

The calculated t- value = 1.09 > 3.19 at 0.025 level of significance

Null hypothesis is rejected

There is sufficient evidence to support the claim that the bags are underfilled

Explanation:

Step(i):-

Given the mean of the Population(μ) = 419 grams

The sample size 'n' =19

Given mean of the sample x⁻ = 412

Given variance of the sample S² = 784

S = √784 = 28

Step(ii):-

Null hypothesis: H₀: There is no sufficient evidence to support the claim that the bags are underfilled.

Alternative hypothesis: H₁:

There is sufficient evidence to support the claim that the bags are underfilled.

Test statistic

`t = (x^(-) -mean)/((S)/(√(n) ) )`

`t = (412 -419)/((28)/(√(19) ) )`

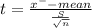
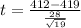
t = -1.09

|t| = |-1.09|

Degrees of freedom ν = n-1 = 19-1 =18

t₀.₀₂₅ = 3.19

Final answer:-

The calculated t- value = 1.09 > 3.19 at 0.025 level of significance

Null hypothesis is rejected

There is sufficient evidence to support the claim that the bags are underfilled