Question

The base of pyramid A is a rectangle with a length of 10 meters and a width of 20 meters. The base of pyramid B is a square with 10-meter sides. The heights of the pyramids are the same.

Answer 1

Explanation:

Given question is incomplete; here is the complete question.

The base of pyramid A is a rectangle with a length of 10 meters and a width of 20 meters. The base of pyramid B is a square with 10-meter sides. The heights of the pyramids are the same.

The volume of pyramid A is ____ the volume of pyramid B. If the height of pyramid B increases to twice that of pyramid A, the new volume of pyramid B is ______the volume of pyramid A.

Since, volume of pyramid =
`(1)/(3)(\text{Area of the base})(\text{Height})`

Volume of the pyramid A =
`(1)/(3)(\text{length}* \text{Width})(\text{height})`

=
`(1)/(3)(10* 20)(h)`

=
`(200h)/(3)`

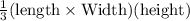
Volume of pyramid B =
`(1)/(3)(10)^2(h)`

=
`(100h)/(3)`

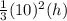
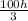
Ratio of the volumes of the pyramids =
`\frac{\text{Volume of pyramid A}}{\text{Volume of pyramid B}}`

=
`((200h)/(3))/((100h)/(3) )`

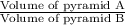
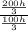
= 2

Therefore, volume of pyramid A is TWICE the volume of pyramid B.

If If height of the pyramid B increases twice of pyramid A,

Then the volume of pyramid B =
`(1)/(3)(100)(2h)`

=
`(200h)/(3)`

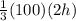
Ratio of volumes of pyramid B and pyramid A =
`\frac{\text{Volume of pyramid B}}{\text{Volume of pyramid A}}`

=
`((200h)/(3))/((200h)/(3))`

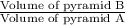
= 1

Therefore, new volume of pyramid B is EQUAL to the volume of pyramid A.