Given:
Area of a circle, A=50.265 sq. units.
Radius of circle, r = 4 units.
To find:
The value of π to the nearest thousandth.
Solution:
Formula for area of a circle is
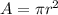

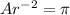
Now, using
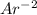 expression, we can find the value of π.
expression, we can find the value of π.
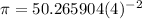
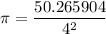


Approximate the value to the nearest thousandth (three digits after decimal).
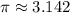
Therefore, the approximated value of π is 3.142.