Answer:
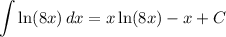
Explanation:
So we have the integral:

First, let's do a substitution to simplify the inside of natural log. Let y equal to 8x. So:
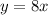
Differentiate with respect to x:
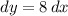
Divide both sides by 8:
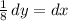
Substitute this into our original integral. Therefore:
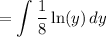
Move the co-efficient outside:
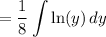
Now, perform integration by parts. Integration by parts is as follows:
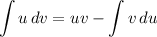
Note that our integral is the same as saying:
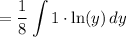
Let u equal the natural log and let dv equal 1 dy. Therefore:
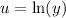
Differentiate:
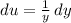
And let dv equal 1 dy. Thus:

Integrate:
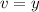
Perform integration by parts:
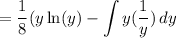
Simplify:
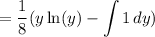
Evaluate the integral:
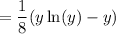
Substitute 8x for y:
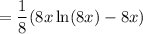
Distribute:
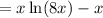
Constant of Integration:
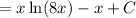
And we have our answer.
Edit: Typo