Question

Seventy cards are numbered 1 through 70, one number per card. One card is randomly selected from the deck. What is the probability that the number drawn is a multiple of 3 AND a multiple of 5?

Answer 1

Given:

Seventy cards are numbered 1 through 70, one number per card. One card is randomly selected from the deck.

To find:

The probability that the number drawn is a multiple of 3 and a multiple of 5.

Solution:

Total number from 1 to 70 = 70

Multiple of 3 from 1 to 70 are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69.

Multiple of 5 from 1 to 70 are 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70.

Numbers which are multiply of both number 3 and 5 = 15, 30, 45, 60

Number of favorable outcomes = 4

`Probability=\frac{\text{Number of favorable outcomes}}{\text{Total number of outcomes}}`

`Probability=(4)/(70)`

`Probability=(2)/(35)`

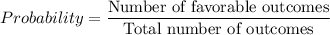
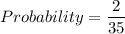
Therefore, the required probability is
`(2)/(35)`.