Answer:
The cost of operating Lee's TV for a month of 30 days is $ 5.4.
Explanation:
Power is the rate of change of energy in time. At first we need to determine monthly energy consumption under the assumption that power remains constant in time:
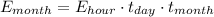
Where:
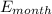 - Monthly energy consumption, measured in watt-hours.
- Monthly energy consumption, measured in watt-hours.
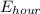 - Hourly consumption rate, measured in watts per hour.
- Hourly consumption rate, measured in watts per hour.
 - Daily time, measured in hours per day.
- Daily time, measured in hours per day.
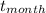 - Number of days within a month, measured in days.
- Number of days within a month, measured in days.
If we know that
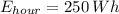 ,
,
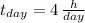 and
and
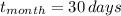 , then:
, then:


A kilowatt-hour equals 1000 watt-hours, then:
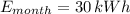
Finally, we get the monthly cost to operate a TV by multiply the result above by electricity unit cost, that is: (1 cent - 0.01 USD)
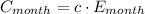
Where:
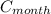 - Monthly energy cost, measured in US dollars.
- Monthly energy cost, measured in US dollars.
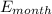 - Monthly energy consumption, measured in kilowatt-hours.
- Monthly energy consumption, measured in kilowatt-hours.
 - Electricity unit cost, measured in US dollars per killowatt-hour.
- Electricity unit cost, measured in US dollars per killowatt-hour.
If we know that
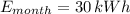 and
and
 , then:
, then:
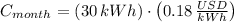
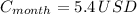
The cost of operating Lee's TV for a month of 30 days is $ 5.4.