Question

Suppose you are navigating a spacecraft far from other objects. The mass of the spacecraft is 2.0 104 kg (about 20 tons). The rocket engines are shut off, and you're coasting along with a constant velocity of ‹ 0, 28, 0 › km/s. As you pass the location ‹ 4, 4, 0 › km you briefly fire side thruster rockets, so that your spacecraft experiences a net force of ‹ 7.0 105, 0, 0 › N for 21 s. The ejected gases have a mass that is small compared to the mass of the spacecraft. You then continue coasting with the rocket engines turned off. Where are you an hour later? (Think about what approximations or simplifying assumptions you made in your analysis. Also think about the choice of system: what are the surroundings that exert external forces on your system?)

Answer 1

r = <2.640 10⁶, 1.01 10⁸, 0> m

Step-by-step explanation:

For this exercise we are going to solve it for each direction separately,

we locate a fixed reference frame in space at the height of the rocket, such that the position of the rocket is

r₀ = <4, 4, 0> 10³ m

X axis

the initial velocity of the ship on this axis is v₀ₓ = 0, when it passes through the point x₀ = 4 km it ignites the rockets, experiencing a force of Fₓ = 7.0 10⁵ N for 21 s and the rockets turn off

They ask where it is after one hour t = 1 h = 3600 s

Let's apply Newton's second law

Fₓ = m aₓ

aₓ = Fₓ / m

aₓ = 7.0 10⁵/2 10⁴

aₓ = 3.5 10¹ m / s

Let's use kinematics to find the distance

for the first t₁ = 21 s the movement is accelerated

x₁ = x₀ + v₀ t₁ + ½ aₓ t₁²

x₁ = x₀ + ½ aₓ t₁²

x₁ = 4000 + ½ 35 21² = 4000 + 7717,.5

x₁ = 11717.5 m

this instant has a speed of

vₓ = v₀ₓ + aₓ t

vₓ = aₓ t ₁

vₓ = 35 21

vₓ = 735 m / s

the rest of the time there is no acceleration so it is uniform motion at this speed

t₂ = 3600 - 21

t₂ = 3576 s

vₓ = x₂ / t₂

x₂ = vₓ t₂

x₂ = 735 3576

x₂ = 2,628 10⁶ m

the total distance traveled in this direction is

x_total = x₁ + x₂

x_total = 11717.5 + 2.628 10⁶

x_total = 2,640 10⁶ m

Y axis

on this axis it is in the initial position of y₀ = 4000 m, with an initial velocity of
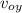`v_(oy)` = 28 10³ m / s and there is no force on this axis F_{y} = 0

The movement in this axis is uniform,

v_{y} = y / t

y = v_{y} t

y = 28 10³/3600

y = 1.01 10⁸ m

the total distance is

y_total = y₀ + y

y_total = 4000 + 1.01 10⁸

y_total = 1.01 10⁸ m

Z axis

the initial position is z₀ = 0, with an initial velocity of v₀ = 0 and in this axis there is no force F_{z} = 0

the movement is uniform

z = 0

the final position of the rocket after 1 h is

r = <2.640 10⁶, 1.01 10⁸, 0> m