Question

Sphere 1 has surface area A₁ and volume V₁, sphere 2 has surface area A₂ and volume V₂. If the radius of sphere 2 is six times the radius of sphere 1, what is the ratio
`(A2)/(A1)` of the areas? What is the ratio
`(V2)/(V1)` of the volumes?

Answer 1

Let , radius of sphere 1 is r .

So , radius of sphere 2 is 6r .

Surface area of sphere is given by :

`A=4\pi r^2`

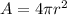
So ,

`(A_2)/(A_1)=(4\pi(6r)^2)/(4\pi r^2)\\\\(A_2)/(A_1)=36`

Volume is given by :

`V=(4)/(3)\pi r^3`

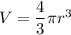
Ratio of sphere 2 by sphere 1 is given by :

`(V_2)/(V_1)=((4)/(3)\pi (6r)^3)/((4)/(3)\pi r^3)\\\\(V_2)/(V_1)=216`

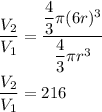
Therefore , the ratio of area and volume is 36 and 216 respectively .

Hence , this is the required solution .